C++ 알고리즘 - DFS, BFS
by 너나나
그래프의 탐색
대표적인 그래프 탐색인 DFS, BFS에 대해서 알아보자.
그래프 탐색의 목적은 임의의 정점에서 시작해서 연결되어있는 모든 정점들을 한 번씩 방문하는 것이다.!

1. DFS (Depth First Search) : 깊이 우선 탐색
스택을 이용해서 갈 수 있는 만큼 최대한 많이 가고 갈 수 없으면 이전 정점으로 돌아가서 모든 정점을 방문한다.
(재귀를 사용할 수도 있다!)

이 그래프에 dfs를 사용해보자.
1에서 시작하고 어떤 정점을 방문하면 스택에 넣고 check[i] 에 1을 표시하자.

현재 정점 : 1
순서 : 1
스택 : 1
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 0 | 0 | 0 | 0 | 0 |
1 다음에 갈 수 있는건 2, 5 둘 중에 하나로 가면 된다. 2로 가보자

현재 정점 : 2
순서 : 1 2
스택 : 1 2
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 0 | 0 | 0 | 0 |
2 다음에 3으로 가보자 (그림은 생략!!)
현재 정점 : 3
순서 : 1 2 3
스택 : 1 2 3
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 0 | 0 | 0 |
3 다음 4로 가보자.
현재 정점 : 4
순서 : 1 2 3 4
스택 : 1 2 3 4
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 1 | 0 | 0 |
4 다음 5로 가보자.
현재 정점 : 5
순서 : 1 2 3 4 5
스택 : 1 2 3 4 5
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 1 | 1 | 0 |

5 다음에는 갈 수 있는 곳이 없다!!(연결된 부분이 다 체크돼있다)
그러면 이제 stack에서 하나씩 pop 하면서 갈 수 있는 곳을 찾아본다.
5에서 pop 하면 4로 간다.
현재 정점 : 4
순서 : 1 2 3 4 5
스택 : 1 2 3 4
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 1 | 1 | 0 |

4에서는 6으로 갈 수 있으니까 6으로 간다.
현재 정점 : 6
순서 : 1 2 3 4 5 6
스택 : 1 2 3 4 6
이러면 이제 모든 정점을 한 번씩 방문했다.
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 1 | 1 | 1 |
6에서 더 이상 갈 데가 없으니까 pop
현재 정점 : 4
순서 : 1 2 3 4 5 6
스택 : 1 2 3 4
4에서도 더이상 갈 데 없으니까 pop
현재 정점 : 3
순서 : 1 2 3 4 5 6
스택 : 1 2 3
3에서도 갈 데 없으니까 pop
현재 정점 : 2
순서 : 1 2 3 4 5 6
스택 : 1 2
2에서도 갈 데 없으니까 pop
현재 정점 : 1
순서 : 1 2 3 4 5 6
스택 : 1
1에서도 갈 데 없으니까 pop 하면
현재 정점 :
순서 : 1 2 3 4 5 6
스택 :
스택이 비었으니까 탐색을 종료한다.
이제 이 과정을 코드로 구현해보자!!
DFS는 재귀 호출을 이용해서 구현할 수 있다.
void dfs(int x) { // dfs(x) : x를 방문
check[x] = true; // x를 방문했으니까 check에 true를 표시
for (int i = 1; i <= n; i++) {
if (a[x][i] == 1 && check[i] == false) { // x에서 i로 가는 edge가 존재하고 아직 그 i를 방문하지 않았으면
dfs(i);
}
}
} // 인접 행렬을 이용한 구현void dfs(int x) {
check[x] = true;
for (int i = 0; i < a[x].size(); i++) {
int y = a[x][i];
if (check[y] == false) {
dfs(y);
}
}
} // 인접 리스트를 이용한 구현시간 복잡도
- 인접 리스트 : O(V + E)
- 인접 행렬 : O(V^2)
인접 행렬을 사용하는 것보다 리스트를 사용하는 게 더 빠르다
2. BFS (Breadth First Search) : 너비 우선 탐색
BFS는 큐를 이용해서 지금 위치에서 갈 수 있는 것을 모두 큐에 넣는 방식이다. 큐에 넣을 때 방문했다고 체크해야 한다.

위에서 본 이 그래프에 bfs를 사용해보자. (1에서 시작한다고 가정)

현재 정점 : 1
순서 : 1
큐 : 1
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 0 | 0 | 0 | 0 | 0 |
1에서 갈 수 있는 곳은 2와 5이다. 얘네를 깡그리 큐에 넣자.
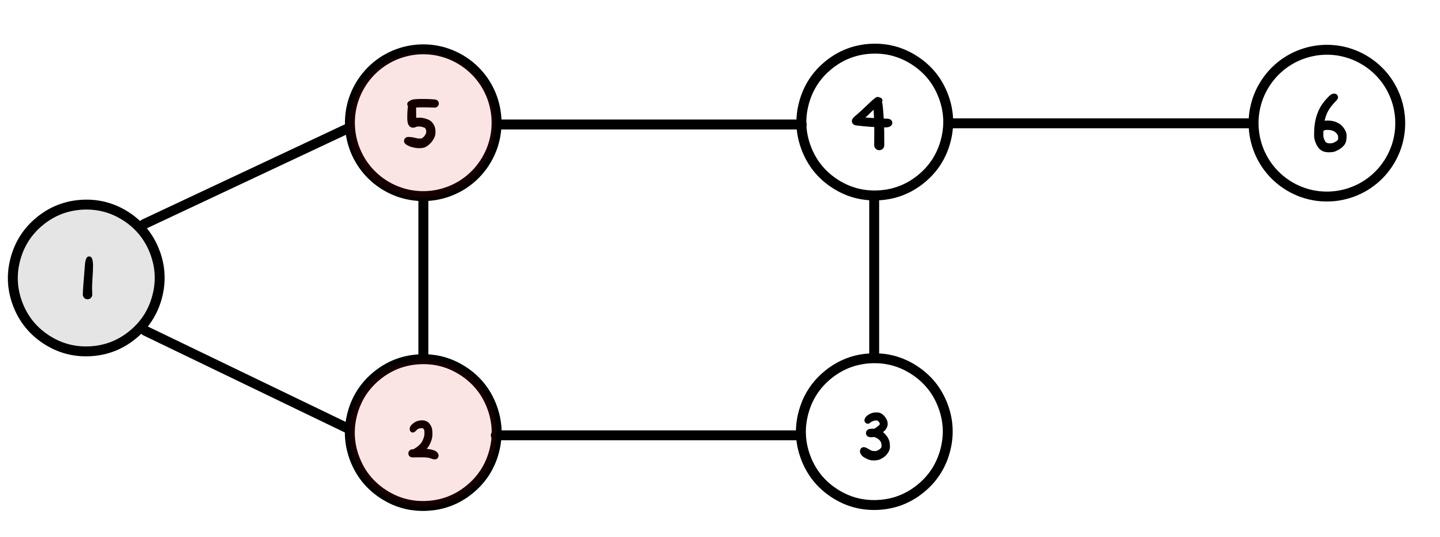
현재 정점 : 1
순서 : 1 2 5
큐 : 1 2 5
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 0 | 0 | 1 | 0 |
그러고 pop 하면 큐의 맨 앞은 2이다.
2에서 갈 수 있는 곳은 3이다. 3을 큐에 넣자.
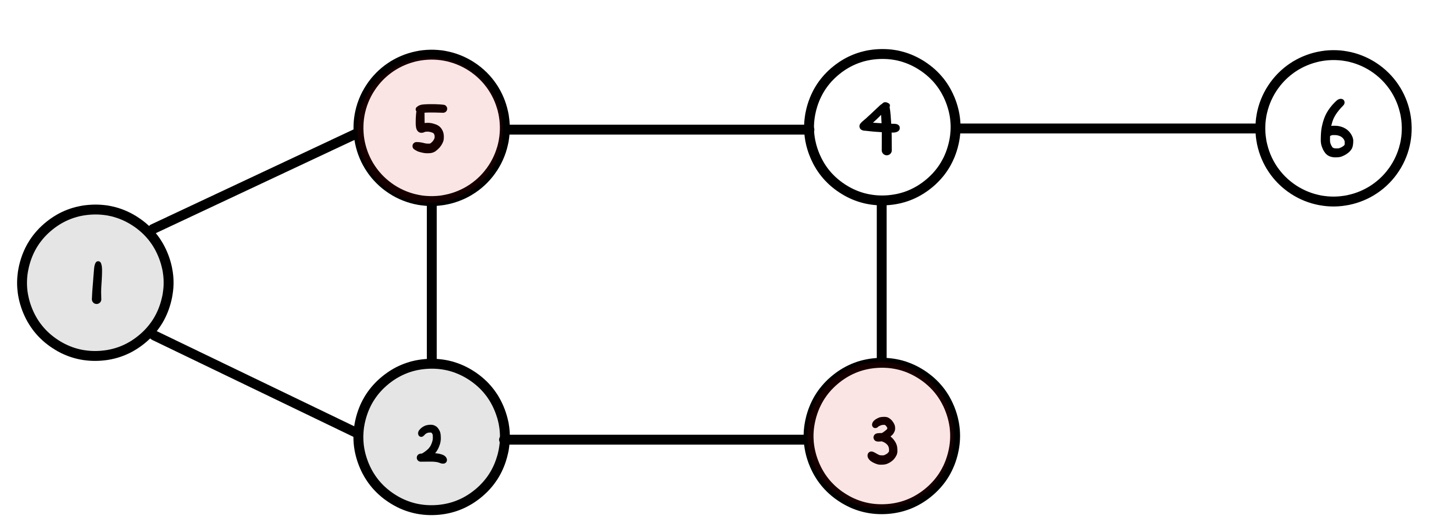
현재 정점 : 2
순서 : 1 2 5 3
큐 : 2 5 3
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 0 | 1 | 0 |
이제 pop 하면 큐의 맨 앞은 5다.
5에서 갈 수 있는 곳은 4이다. 4를 큐에 넣자.
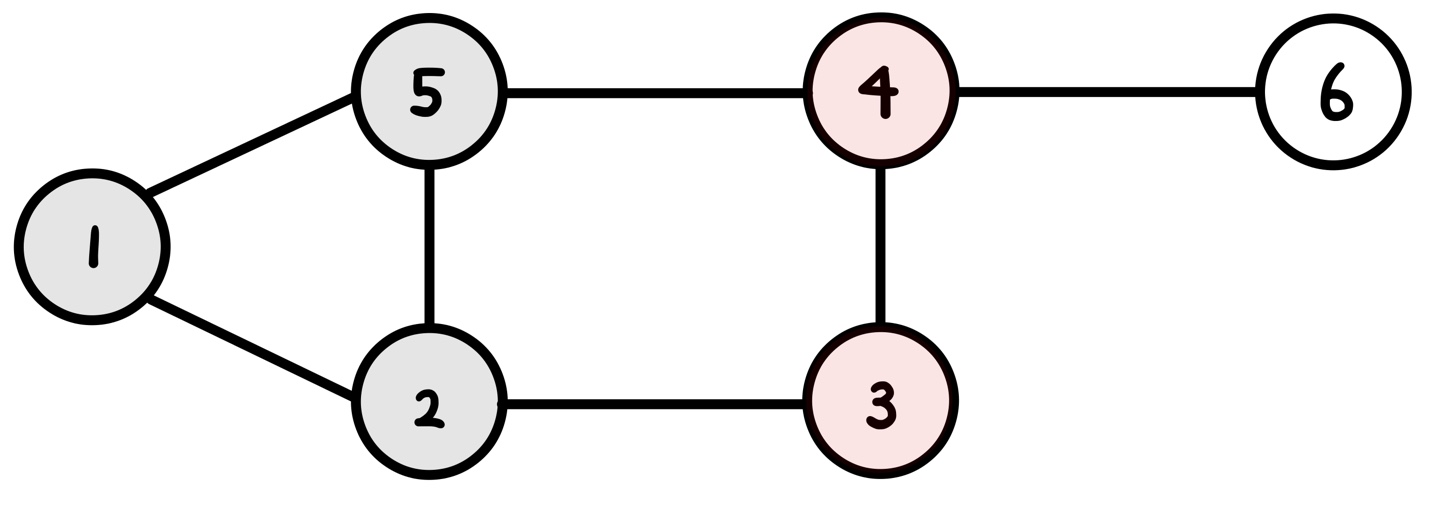
현재 정점 : 5
순서 : 12 5 3 4
큐 : 5 3 4
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 1 | 1 | 0 |
이제 pop 하면 큐의 맨 앞은 3이다. 3은 더 이상 갈 수 있는 곳이 없으므로 pop 한다.
그럼 큐의 맨 앞은 4이다. 4에서 갈 수 있는 곳은 6이다. 6을 큐에 넣자.
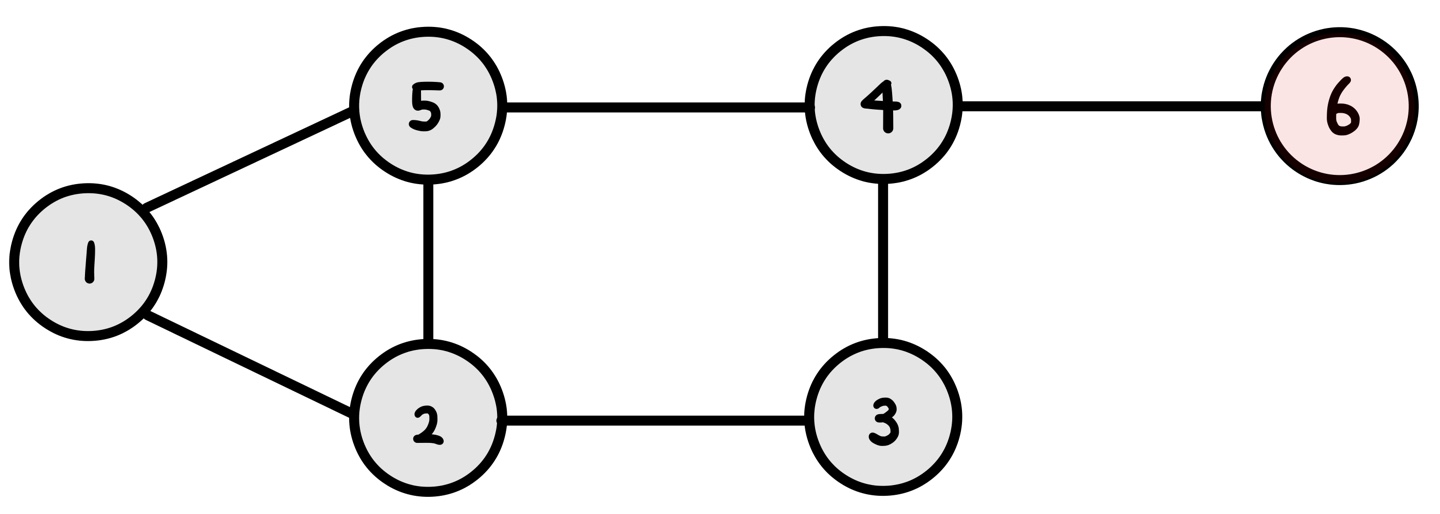
현재 정점 : 4
순서 : 12 5 3 4 6
큐 : 4 6
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| check[i] | 1 | 1 | 1 | 1 | 1 | 1 |
이제 pop 하면 큐의 맨 앞은 6이고 6은 더 이상 갈 수 있는 곳이 없으므로 pop 한다.
그러면 큐가 비었으므로 탐색을 종료한다.
이 과정들을 코드로 구현해보자.
queue<int> q;
check[1] = true;
q.push(1); // 1부터 시작
while (!q.empty()) {
int x = q.front(); q.pop();
for (int i = 1; i <= n; i++) {
if (a[x][i] == 1 && check[i] == false) { // x에서 갈 수 있고 아직 방문하지 않은 곳
check[i] = true; // 방문
q.push(i);
}
}
} // 인접 행렬을 이용한 구현queue<int> q;
check[1] = true;
q.push(1);
while (!q.empty()) {
int x = q.front(); q.pop();
for (int i = 0; i < a[x].size(); i++) {
int y = a[x][i];
if (check[y] == false) {
check[y] = true;
q.push(y);
}
}
} // 인접 리스트를 이용한 구현시간 복잡도
- 인접 리스트 : O(V + E)
- 인접 행렬 : O(V^2)
BFS도 마찬가지로 인접 행렬을 사용하는 것보다 인접 리스트를 사용하는 게 더 빠르다.
'study > 알고리즘' 카테고리의 다른 글
| C++ 백준 2667번 (0) | 2021.01.13 |
|---|---|
| C++ 백준 11724번 (0) | 2021.01.13 |
| C++ 자료구조 - 그래프 (0) | 2021.01.12 |
| C++ 백준 10971번 (0) | 2021.01.11 |
| C++ 백준 10972번 (0) | 2021.01.08 |
블로그의 정보
공부 기록
너나나