[자료구조] 이진 검색
by 너나나정렬된 맵
맵의 엔트리들을 어떤 전체 순서(total order)에 따라 정렬하고, 이렇게 정렬된 순서에 따라 키와 값을 검색하는 정렬된 맵을 사용할 필요가 있다.
- firstEntry(k): 가장 작은 키값을 가진 엔트리에 대한 반복자를 반환. 맵이 비었다면 end를 반환
- lastEntry(k): 가장 큰 키값을 가진 엔트리에 대한 반복자를 반환. 맵이 비었다면 end 반환
- ceilingEntry(k): k보다 크거나 같은 키값 중 가장 작은 키값을 가진 엔트리에 대한 반복자를 반환. 그런 엔트리가 없다면 end 반환
- floorEntry(k): k보다 작거나 같은 키값 중 가장 큰 키값을 가진 엔트리에 대한 반복자 반환. 그러한 엔트리 없다면 end 반환
- lowerEntry(k): k보다 작은 키값 중 가장 큰 키값을 가진 엔트리에 대한 반복자를 반환. 그러한 엔트리 없다면 end 반환
- higherEntry(k): k보다 큰 키값 중 가장 작은 키값을 가진 엔트리에 대한 반복자 반환. 그러한 엔트리 없다면 end 반환

만약 맵의 키들이 전체 순서(total order) 관계를 가지면, 우리는 맵의 엔트리들을 벡터 L에 키들이 증가하는 순서로 저장할 수 있다. 맵의 정렬된 벡터 구현을 정렬된 검색 테이블(ordered search table)이라 부른다.
정렬된 검색 테이블의 요구 공간은 O(n)이다. 비정렬 리스트와는 다르게 검색 테이블의 수정은 시간이 많이 소요된다. 특히 검색 테이블에서 insert(k, v) 연산을 수행하는 데 최악의 경우 O(n) 시간이 필요하다. 새 엔트리 (k, v)가 들어갈 자리를 만들기 위해 벡터 내에 k보다 큰 키를 가진 모든 엔트리를 한 칸씩 움직여야 하기 때문이다. erase(k) 연산도 삭제된 엔트리가 남긴 빈자리를 채우기 위해 벡터 내에서 k보다 큰 키를 가진 모든 엔트리를 움직여야 한다. 따라서 검색 테이블 구현은 맵 수정 연산의 최악의 경우 실행 시간은 연결 리스트보다 나쁘다. 하지만 find 연산은 검색 테이블에서 훨씬 빠르게 수행된다.
이진 검색
정렬된 벡터 L을 이용하여 n개의 엔트리를 갖는 맵을 구현하는 방법의 장점은 L의 원소를 인덱스에 의해 O(1) 시간에 접근할 수 있다는 점이다. 벡터에서 어떤 원소의 인덱스는 그것보다 앞에 있는 원소의 개수이다. 따라서 L의 첫 번째 원소는 인덱스 0이고 마지막 원소는 인덱스 n - 1이다. 정렬된 검색 테이블에서 엔트리를 찾는 고전적인 알고리즘인 이진 검색(binary search)를 보자!!
L의 원소들은 맵의 엔트리들이다. 그리고 L이 정렬되어 있기 때문에 인덱스 i에 있는 엔트리는 인덱스 0, ..., i - 1에 있는 엔트리들보다 작지 않고 i + 1, ..., n - 1에 있는 엔트리들보다 크지 않다.
그림으로 설명해본다!!!! 우리가 찾는 엔트리의 키를 k라고 하자. L에는 총 n개의 엔트리가 있다.
첫 번째 엔트리를 low, 마지막 엔트리를 high라고 지정했다!!

이제 우리는 키 값이 k인 엔트리를 찾을 것이다. 이 배열의 중간 인덱스는 ⌊(low+high)/2⌋이다.
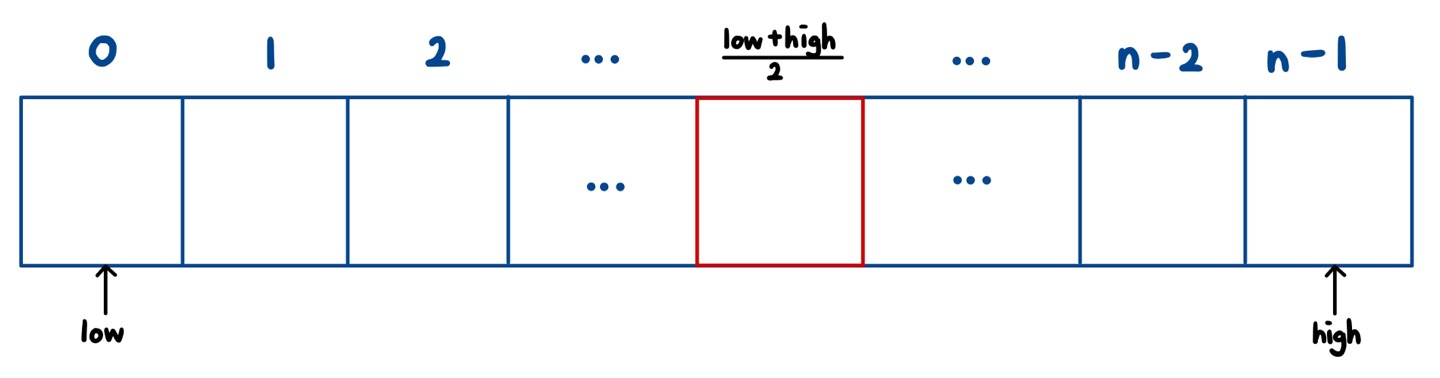
저 중간 인덱스를 mid라고 하자. mid를 기준으로 왼쪽들은 mid보다 키값이 작고 오른쪽은 mid보다 키 값이 클것이다. 따라서 mid.key()와 k값을 비교하여 k 값이 크면 low를 mid 다음으로 옮기고, k값이 작다면 high를 mid의 왼쪽으로 옮긴다. 같다면 mid에서 엔트리를 찾을 수 있다.
그림으로 보자!!
만약 mid.key값이 k값이 크다면
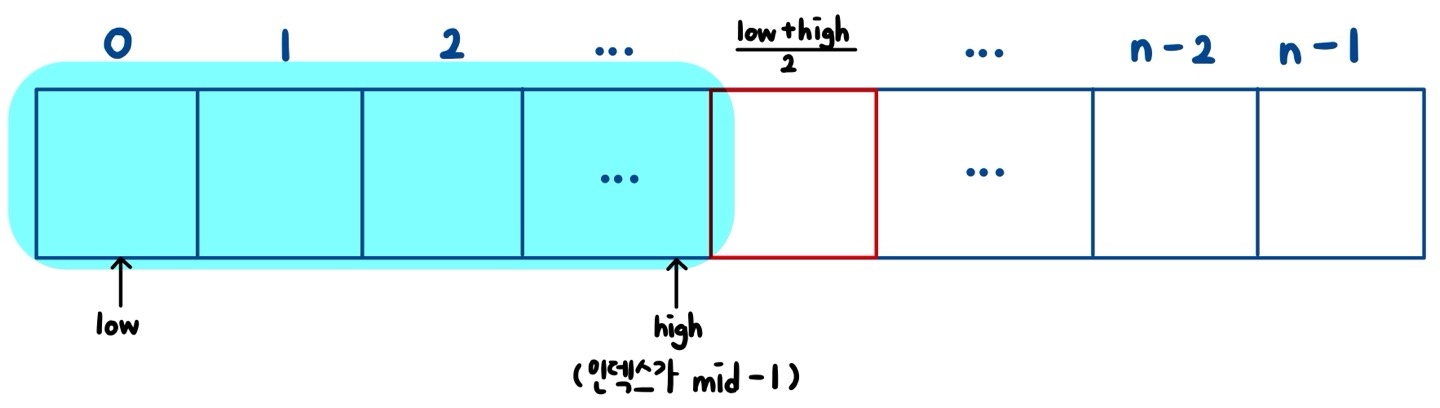
이 색깔이 칠해져 있는 배열만 조사하면 된다!! 왜냐면 어짜피 mid의 오른쪽 부분은 이 키값보다 더 큰 애들만 있을 테니까 mid보다 키 값이 작은 부분에서 k값을 찾을수 있다!!!! 여기는 키 값대로 정렬되어있으므로!!!! 그래서 low는 그대로 두고 high를 mid-1로 옮겨서 범위를 mid보다 키값이 작은 배열들만 조사하는 것으로 좁히는 것이다.
반대로 mid.key값이 k값보다 작다면
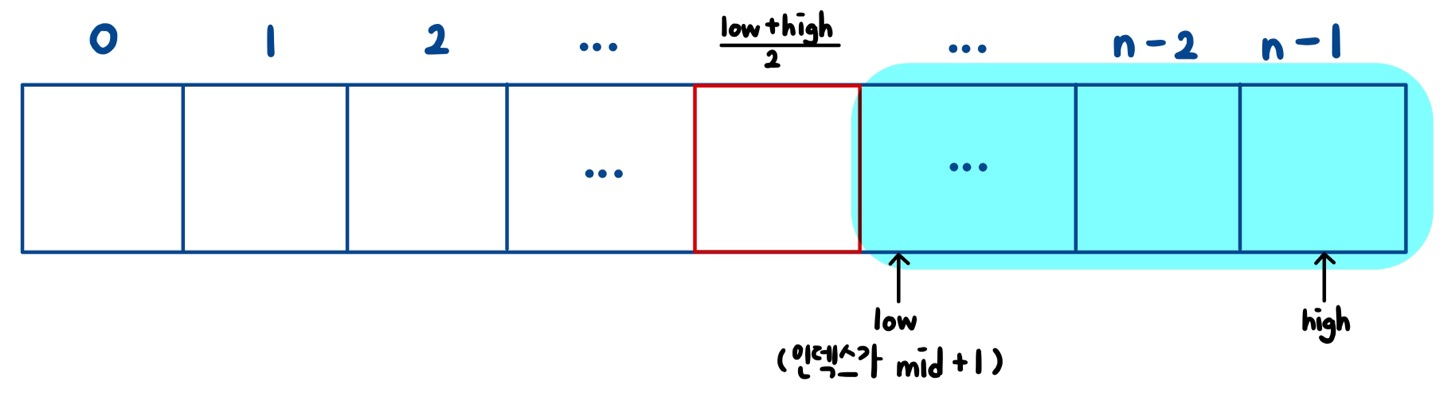
이 색깔이 칠해져 있는 배열만 조사하면 된다!! mid의 왼쪽 부분은 이 키값보다 작은 애들만 모여있을테니까 볼 필요가 없지!!! k가 mid보다 크니까 mid보다 큰 쪽에서 k를 찾는 것이다. 그래서 여기서는 high를 그대로 두고 low를 mid+1로 옮겨서 mid보다 큰 키값을 데리고 있는 배열들만 조사하는 것으로 범위를 좁혔다!!
이렇게 중간에 있는 키값보다 k값이 크냐 안크냐를 따져보고 범위를 계속해서 좁혀나가면 된다!!!
만약 mid.key가 k와 같다면 엔트리를 찾은거니까 더 생각할 필요없이 종료하면 된다!!! 그래서 이걸 정리하면
초기에 low = 0, high = n - 1이고 k를 중간 엔트리의 키와 비교한다. 이때 중간 엔트리를 e, 인덱스를 mid라고 하면 mid = ⌊(low+high)/2⌋이다. 다음과 같은 세가지 경우가 발생한다.
- 만약 k = e.key()이면 찾고자 하는 키를 찾은 것이므로 e를 반환하고 검색을 성공적으로 종료한다.
- 만약 k < e.key()이면 찾고자 하는 엔트리가 e의 앞에 있는 경우(반으로 나눈 것들 중 앞에꺼)이다. 따라서 인덱스 low부터 mid-1까지 다시 검색한다.
- 만약 k > e.key()이면 찾고자 하는 엔트리가 e의 뒤에 있는 경우(반으로 나눈 것들 중 뒤에꺼)이다. 따라서 인덱스 mid+1부터 high까지 다시 검색한다.
이제 수도 코드로 보자!!
Algorithm BinarySearch(L, k, low, high): input: n개의 엔트리를 저장한 정렬된 벡터 L과 검색하고자 하는 키 k 그리고 정수 low와 high output: L의 인덱스 low와 high 사이에서 키값으로 k를 갖는 엔트리, 존재하지 않다면 특수 센티널 end if low > high then 이게 교차되는 순간 엔트리가 존재하지 않다는 것 return end else mid <- ⌊(low+high)/2⌋ e <- L.at(mid) mid에 위치하는 엔트리 if k = e.key() then return e else if k < e.key() then return BinarySearch(L, k, low, mid - 1) else return BinarySearch(L, k, mid + 1, high)이진 검색을 실행하면 호출될 때 마다 후보 엔트리의 수(키값으로 k를 가질 수 있는 가능성이 있는 엔트리들)가 반으로 감소한다. 따라서 이진검색의 실행시간은 O(logn)이다.
참고 문헌
[1] Michael T. Goodrich, Roberto Tamassia, Davaid M. Mount, C++로 구현하는 자료구조와 알고리즘, WILEY, 2013.
'2022 > 자료구조 + 알고리즘' 카테고리의 다른 글
| [자료구조] 이진 탐색트리 (0) | 2022.01.20 |
|---|---|
| [자료구조] 맵, 해시 테이블 (0) | 2022.01.19 |
| [자료구조] 힙 정렬 (0) | 2022.01.18 |
| [자료구조] 힙 (0) | 2022.01.18 |
| [자료구조] 우선순위 큐 (0) | 2022.01.16 |
블로그의 정보
공부 기록
너나나