[자료구조] 힙
by 너나나https://guiyum.tistory.com/130
[자료구조] 우선순위 큐
우선순위 큐 : 임의의 순서로 입력된 우선순위된 원소들을 저장하고 우선순위에 따라 출력하는 추상 데이터 타입 저장된 원소들 중 가장 우선순위가 높은 원소가 삭제됨 키 응용프로그램에서는
guiyum.tistory.com
▲우선순위 큐는 전 포스팅
힙(Heap)
: 키들을 내부 노드들에 저장하는 이진 트리 T. 다음과 같은 특성을 가진다.
- 힙-순서 특성(Heap-Order Property): 힙 T에서 루트를 제외한 모든 노드 v에 대하여 v에 저장된 키는 v의 부모에 저장된 키보다 크거나 같다. => 최소값을 갖는 키는 항상 T의 루트에 저장된다.
- 완전(complete) 이진 트리 특성: 힙은 완전(complete)해야 한다. -> 레벨 0, 1, 2, ..., h-1들이 가질 수 있는 최대 수의 노드를 포함하고 (레벨 i는 2^i 노드를 포함, 이떄 0 ≤ i ≤ h - 1) 레벨 h - 1에서 모든 내부 노드는 외부 노드들의 왼쪽에 위치한다면, 높이 h인 이진 트리 T는 완전하다.)

힙의 높이(Height)
T의 높이를 h라 하자. 어떤 노드가 레벨 h에 있으며 같은 레벨의 다른 노드들이 모두 그 노드의 왼쪽에 있을 때 그것을 T의 마지막 노드라고 한다.
n개를 저장하는 힙 T의 높이는 다음과 같다.

증명: T가 완전하므로, 각 레벨 i(0 ≤ i ≤ h - 1)에 2^i개의 노드가 있고 레벨 h에는 적어도 하나의 노드가 있다. 따라서 T의 노드 수는 적어도
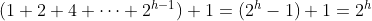
레벨 h는 최대 2^h개의 노드를 가진다, 따라서 T의 최대 노드 수는

노드 수는 전체 키의 수 n과 같으므로,

그리고

위 두 식의 양변에 로그를 취하면,
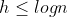
그리고

h는 정수이므로, 다음 식이 성립한다.

완전(Complete) 이진트리와 표현

- add(e): T에 추가하고 원소 e를 저장하는 새로운 마지막 노드 v를 반환한다. 새롭게 만들어진 T는 v를 마지막 노드로 갖는 완전 이진트리이다.
- remove(): T의 마지막 노드를 삭제하고 그 노드를 반환한다.
이 연산들만을 사용함으로써 트리 T는 계속 완전 이진트리로 유지된다. add의 효과는 두 가지 경우가 있다.
- 만약 T의 바닥 레벨이 꽉 차지 않았다면, add는 T의 바닥 레벨의 가장 오른쪽에 있는 노드(= 마지막 노드)의 바로 다음에 새 노드를 삽입한다. 따라서 T의 높이는 변하지 않는다.
- 만약 T의 바닥 레벨이 꽉 찼다면, add는 T의 바닥 레벨의 가장 왼쪽에 있는 노드의 왼쪽 자식으로 새 노드를 삽입한다. 따라서, T의 높이는 1 증가한다.
완전 이진 트리의 벡터 표현
https://guiyum.tistory.com/129
[자료구조] 이진 트리
이진 트리 : 모든 노드가 최대로 두 개의 자식 노드를 갖는 순서화된 트리 각 노드가 최대 2개의 자식을 갖는다. 각 노드가 자식을 왼쪽 자식 또는 오른쪽 자식으로 분류한다. 왼쪽 자식이 오른쪽
guiyum.tistory.com
여기서 말한 벡터 기반 이진트리의 표현이 완전 이진트리 T의 표현에 특히 적절하다.

T의 노드를 벡터 A에 저장하는데 인덱스는 다음과 같은 레벨 번호 f(v)와 같다.
- 만약 v가 T의 루트이면, f(v) = 1
- 만약 v가 노드 u의 왼쪽 자식이면, f(v) = 2f(u)
- 만약 v가 노드 u의 오른쪽 자식이면, f(v) = 2f(u) + 1
완전 이진트리의 벡터-기반한 표현의 단순함으로 인해 함수 add와 remove의 구현에 도움이 된다. 배열의 확장이 필요하지 않다고 가정하면, 함수 add와 remove는 벡터의 마지막 원소를 추가하거나 삭제하기 때문에 O(1) 시간에 실행된다. 또한 T와 연관된 벡터는 n + 1개의 원소를 갖는다(인덱스 0은 사용하지 않는다.)
만약 벡터의 구현에 크기를 줄이거나 늘릴 수 있는 확장 가능한 배열을 사용한다면(ex. 벡터), n개의 노드를 갖는 완전 이진트리의 벡터-기반한 표현에 필요한 공간은 O(n)이고 add, remove는 O(1)의 할부된(amortized) 시간이 소요된다.
완전 이진 트리의 C++ 구현
template <typename E>
class VectorCompleteTree {
// ... private 멤버 데이터와 protected 함수들을 이곳에 삽입
public:
VectorCompleteTree() : V(1) {} // 생성자
class Position; // 노드 위치 타입
int size() const { // 원소의 개수
return V.size() - 1;
}
Position left(const Position& p) { // 왼쪽 자식을 구하라
return pos(2*idx(p));
}
Position right(const Position& p) { // 오른쪽 자식을 구하라
return pos(2*idx(p) + 1);
}
Position parent(const Position& p) { // 부모를 구하라
return pos(idx(p)/2);
}
bool hasLeft(const Position& p) const { // 왼쪽 자식을 가졌는가?
return 2*idx(p) <= size();
}
bool hasRight(const Postion& p) const { // 오른쪽 자식을 가졌는가?
return 2*idx(p) + 1 <= size();
}
bool isRoot(const Position& p) const { // 루트?
return idx(p) == 1;
}
Position root() { // 루트 위치를 구하라
return pos(1);
}
Position last() { // 마지막 노드를 구하라
return pos(size());
}
void addLast(const E& e) { // 새로운 마지막 노드 추가
V.push_back(e);
}
void removeLast() { // 마지막 노드를 삭제
V.pop_back();
}
void swap(const Position& p, const Position& q) { // 노드 내용을 서로 교환
E e = *q;
*q = *p;
*p = e;
};
// 완전 이진트리를 위한 인터페이스 CompleteBinaryTree
힙을 이용한 우선순위 큐의 구현
우선순위 큐p를 위한 힙 자료구조는 다음을 포함한다.
- heap: 완전 이진 트리 T로서 원소들이 힙-순서 특성에 따라 내부 노드에 저장되어 있다. T의 각 내부 노드 v에 각 원소의 키 k(v)가 저장되어 있다.
- comp: 키 간의 전체 순서 관계를 정의하는 비교자

삽입
힙 T를 이용하여 우선순위 큐의 insert 함수의 구현 방법을 알아보자. 새로운 원소 e를 T에 삽입하기 위하여 함수 add로 T에 새로운 내부 노드를 추가하여 새 노드가 T의 마지막 노드가 되게 한 후 e를 이 노드에 저장한다. 이러한 작업 뒤에 트리 T는 완전하나 힙-순서 특징을 위반하고 있을 수 있다. 따라서 노드 z가 T의 루트가 아니면 키 k(z)를 z의 부모 u의 키 k(u)와 비교한다. 만약 k(u) > k(z)이면, 이 둘을 교환하여 힙-순서 특성을 복구해야 한다. 이 교환으로 인해 새로운 키-원소 쌍 (k, e)가 한 레벨 상승하게 된다. 이러한 교환을 더 이상 힙-순서 특성의 위반이 없을 때까지 T의 상위 레벨로 계속한다.
이러한 교환을 업-힙 버블링(up-heap bubbling)이라 한다. 최악의 경우, 업-힙 버블링에 의하여 새로운 키-원소 쌍이 T의 루트까지 계속 움직이게 된다. 따라서 최악의 경우에 insert 함수에 의해 원소가 교환되는 횟수는 T의 높이와 같다. 즉


삭제

힙에서 가장 작은 노드를 삭제하려면 루트 노드를 삭제한다. 그 후 마지막 노드를 루트로 보내고 다운-힙 버블링을 해 힙-순서 특성을 만족시키게 한다. 여기서 r은 T의 루트를 나타낸다.
- 만약 r이 오른쪽 자식이 없으면, s를 r의 왼쪽 자식으로 한다.
- r이 두 자식을 가지고 있다면, 가장 작은 키를 가진 자식을 s라 한다.
만약 k(r) ≤ k(s)이고 힙-순서 특성을 만족한다면 알고리즘을 종료한다. k(r) > k(s) 이면 r과 s에 저장된 엔트리를 교환함으로써 힙-순서 특성을 교환할 필요가 있다. 이러한 교환을 힙-순서 특성의 위반이 없을 때까지 T의 하위 레벨로 계속한다. 이러한 교환에 의한 아래방향으로의 움직임을 다운-힙 버블링(down-heap bubbling)이라 한다. 최악의 경우 키-원소 쌍들이 T의 바닥까지 아래로 움직이게 된다. 최악의 경우 removeMin 함수에 의해 원소가 교환되는 횟수는 T의 높이와 같다. 즉

분석
두 키가 O(1) 시간에 비교되고 힙 T가 벡터 또는 링크드 구조로 구현되었다는 가정하에 우선순위 큐의 힙 구현에 대한 우선순위 큐 ADT 함수들의 실행 시간을 보자!!
| 함수 | 실행 시간 |
| size, empty | O(1) |
| min | O(1) |
| insert | O(log n) |
| removeMin | O(log n) |
결론적으로 힙은 우선순위 큐 ADT를 구현하는 매우 효율적인 자료구조이다. 시퀀스에 기반한 우선순위 큐와는 다르게, 힙 구현은 삽입과 삭제 모두 빠르게 시행한다. 이러한 효율적인 힙 구현으로 인하여 시퀀스에 기반한 삽입-정렬이나 선택-정렬보다 매우 빠르게 우선순위-큐 정렬을 실행할 수 있다.
C++ 구현
힙은 벡터-기반 완전 트리로 구현되었다.
template <typename E, typename C>
class HeapPriorityQueue {
public:
int size() const { // 원소의 개수
return T.size();
}
bool empty() const { // 큐가 비었는지
return size() == 0;
}
void insert(const E& e) { // 원소 삽입
T.addLast(e); // e를 힙에 추가
Position v = T.last(); // e의 위치
while (!T.isRoot(v)) { // 업-힙 버블링
Position u = T.parent(v) // v의 부모를 u
if (!isLess(*v, *u)) break; // v의 순서 특징이 맞으면 루프 종료
T.swap(v, u); // 그렇지 않으면 부모와 교환
v = u;
}
const E& min() { // 최소 원소
return *(T.root());
}
void removeMin() { // 최소값 삭제
if (size() == 1) // 노드가 하나라면 걔 삭제
T.removeLast();
else {
Position u = T.root(); // 루트 위치 저장
T.swap(u, T.last()); // 마지막 노드와 루트 교환
T.removeLast(); // 마지막 노드 삭제
while (T.hasLeft(u)) { // 다운-힙 버블링
Position v = T.left(u);
if (T.hasRight(u) && isLess(*(T.right(u)), *v))
v = T.right(u); // v는 u보다 더 작은 자식
if (isLess(*v, *u)) { // v의 키가 u의 키보다 작은지
T.swap(u, v);
u = v;
}
else break; // 아니면 종료
}
private:
VectorcompleteTree<E> T; // 우선순위 큐의 내용
C isLess; // less-than 비교자
typedef typename VectorCompleteTree<E>::Position Position;
};참고 문헌
[1] Michael T. Goodrich, Roberto Tamassia, Davaid M. Mount, C++로 구현하는 자료구조와 알고리즘, WILEY, 2013.
'2022 > 자료구조 + 알고리즘' 카테고리의 다른 글
| [자료구조] 맵, 해시 테이블 (0) | 2022.01.19 |
|---|---|
| [자료구조] 힙 정렬 (0) | 2022.01.18 |
| [자료구조] 우선순위 큐 (0) | 2022.01.16 |
| [자료구조] 이진 트리 (0) | 2022.01.14 |
| [자료구조] 트리 순회 알고리즘 (전위, 후위) (0) | 2022.01.12 |
블로그의 정보
공부 기록
너나나