[자료구조] 트리 순회 알고리즘 (전위, 후위)
by 너나나깊이와 높이
p를 트리 T의 노드라고 하자!! p의 깊이(depth)는 p의 조상의 수이다.

예를 들어 이 트리의 2의 깊이는 2다!!! (조상 7, 2)
노드 p의 깊이를 다음과 같이 재귀적으로 정의할 수 있다.
- 만약 p가 루트이면, p의 깊이는 0이다.
- 그렇지 않으면, p의 깊이는 p의 부모의 깊이에 1을 더한 것과 같다.
Algorithm depth(T, p):
if p.isRoot() then
return 0
else
return 1 + depth(T, p.parent())수도 코드로 나타내면 이렇게!!!
C++ 코드로 작성해보자!!
int depth(const Tree& T, const Position& p) {
if (p.isRoot())
return 0;
else
return 1 + depth(T, p.parent());
}알고리즘 depth(T, p)의 실행 시간은 위의 알고리즘이 p의 각 조상에 대해 상수 시간의 재귀적 단계를 수행하기 때문에,

이고, 여기서 dp는 트리 T 내에서 노드 p의 깊이를 의미한다. 따라서, 최악의 경우에는 depth 알고리즘은 O(n) 실행 시간을 갖는다. 여기서 n은 트리 T의 총 노드 개수이다.
트리 T에서 노드 p의 높이(height)도 역시 재귀적으로 정의된다!!
- 만약 p가 외부노드이면 p의 높이는 0이다.
- 그렇지 않으면 p의 높이는 p의 자식의 높이 중 가장 높은 값에 1을 더하면 된다.
트리 T의 높이는 T의 루트의 높이이다. (=트리 T의 높이는 T의 외부 노드의 최대 깊이와 같다)
근데 어디서는 높이를 깊이라고도 하고 이거 정의로 봤을때는 약간 최대 자손의 수 같기도 하고?? 뭔가 명확한 정의가 나온 곳이 없네?? 트리의 높이는 노드의 최대 깊이다!!!)
Algorithm height1(T):
h = 0;
for each p in T.positions() do
if p.isExternal() then
h = max(h, depth(T, p))
return h외부 코드의 최대 깊이를 계산하여 트리 T의 높이를 계산하는 알고리즘이다!!
얘를 이제 C++로 구현해보자!!
int height1(const Tree& T) {
int h = 0;
PositionList nodes = T.positions(); // 모든 노드의 리스트
for (Iterator q = nodes.begin(); q != nodes.end(); q++) {
if (q->isExternal()) h = max(h, depth(T, *q); // 리프들 중에 최대 깊이를 구한다
}
return h;
}이 알고리즘 height1은 그다지 효율적이지 않다. height1은 T의 각 외부 노드 p에서 알고리즘 depth(p)를 호출하기 떄문에 height1의 실행 시간은

로 나타낸다!! 여기서 n은 T의 노드 수, d_p는 노드 p의 깊이, E는 T의 외부 노드의 집합이다. 최악의 경우

이기 때문에 알고리즘 height1은 O(n^2) 시간이 걸린다.
높이의 재귀적인 정의를 이용하여 좀 더 효율적인 방법으로 트리 T의 높이를 계산하자!!!
Algorithm height2(T, p):
if p.isExternal() then
return 0
else
h = 0
for each q in p.children() do
h = max(h, height2(T, q))
return 1 + hint height2(const Tree& T, const Position& p) {
if (p.isExternal()) return 0; // 리프의 높이는 0이다!!!
int h = 0; //
PositionList ch = p.children(); // 자식의 리스트
for (Iterator q = ch.begin(); q != ch.end(); q++)
h = max(h, height2(T, *q));
return 1 + h; // 1 + 자식의 높이의 최대값
}알고리즘 height2는 알고리즘 height1보다 효율적이다. height2는 재귀적이며, 만약 얘가 T의 루트에서 호출된다면 결국 T의 각 노드에 대해 한 번씩은 호출되게 된다. 따라서 우리는 먼저 각 노드(비 재귀적인 부분)에서 소비된 총 시간을 결정하고 모든 노드에 걸쳐 이 시간을 합하는 것으로 이 함수의 실행 시간을 결정할 수 있다!! 반복자 children(p)의 시간은

시간이 걸리고, 여기서 c_p는 p의 자식 노드 개수를 의미한다. 또한 while 루프는 반복 횟수 c_p를 가지고 있으며, 루프의 각 반복은 O(1) 시간에다 p의 각 자식 노드에서 재귀적인 호출을 위한 시간을 더한 시간이 걸린다. 따라서, 알고리즘 height2는 각 노드 v에서

시간이 걸리고 실행 시간은

이다!! T를 n개의 노드를 가진 트리라 하고 c_p는 트리 T의 노드 p의 자식의 개수라고 하면
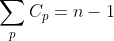
이다. 따라서 height2의 실행 시간은 T의 루트에서 호출될 때 O(n) 이고, 이때 n은 T의 노드 개수이다.
전위 순회(Preorder Traversal)
트리 T의 순회(traversal)는 T의 모든 노드를 "방문"하거나 접근하기 위한 체계적인 방법을 말함
트리 T의 전위 순회에서는 T의 루트가 첫 번째로 방문된 후, 자신의 자식 노드를 루트로 하는 서브 트리들을 재귀적으로 순회한다. 만일 트리가 순서화되어 있다면, 자식들의 순서에 따라 서브 트리가 순회된다.
Algorithm preorder(T, p):
perform the "visit" action for node p
for each child q of p do
recursively traverse the subtree rooted at q by calling preorder(T, q)전위 순회 알고리즘은 부모가 순서에서 자식들보다 항상 전에 와야 하는 트리 노드의 선형순서화에 유용하다!

위처럼 어떤 큰 주제에 소주제를 가지고 발표하는 경우도 트리의 전위 순회 형식이라고 볼 수 있다!!
전위 순회는 트리의 모든 노드를 탐색하기 위한 효과적인 방법이다. 노드 방문 시간이 O(1)이라고 가정하고 n 개의 노드를 가진 트리 T의 전위 순회의 실행 시간을 생각해보자!!
전위 순회 알고리즘은 height2와 유사하다. 각 노드 p에서 전위 순회 알고리즘의 비 재귀적인 부분은

시간을 필요로 하며 이때 c_p는 p의 자식 노드들의 개수이다. 따라서 T에 에 대한 전위 순회의 전체 실행 시간은 O(n)이다.
T에서 노드 p의 서브 트리에서 원소들을 전위 출력하는 함수를 생각해보자! 즉, p를 루트로 하는 서브 트리의 전위 순회를 실행하고 각 노드에 방문될 때 노드의 원소를 출력하는 함수!!
void preorderPrint(const Tree& T, const Position& P) {
cout << *p; // 해당 노드의 원소 출력
PositionList ch = p.children(); // 자식 리스트를 만듦
for (Iterator q = ch.begin(); q != ch.end(); q++) {
cout << " ";
preorderPrint(T, q);
}
}트리의 자식들을 방문할 때 해당 자손들을 괄호로 묶는 괄호 문자열 표현 함수 parenPrint()를 만들어보자!!
이게 무슨 뜻이냐면

위에서 사용한 그림인데 또 데려왔다!! 얘를 괄호 문자열 표현하면
2(7(2 6 (5 11))5(9(4))) 이렇게!!!!!!!!! 되는!!!!!!!! 노드의 자손들을 묶는거라고 보면 된다!!! 2의 자손이 7, 2, 6, 5, 11, 5, 9, 4 니까 얘네를 순회하기 시작할 때 괄호를 열었고 자손들 순회가 끝났을때 괄호를 닫고 2의 자식인 7의 자손은 2, 6, 5, 11이니까 얘네를 괄호로 묶고 ... 이런 식!!
이 알고리즘을 c++로 작성해보자!!
void parenPrint(const Tree& T, const Position& p) {
cout << *p; // 방문한 노드의 원소 출력
if (!p.isExternal()) { // 이놈이 자식이 있으면
PostionList ch = p.children(); // 자식을 리스트에 넣음
cout << "( "; // 자식들 순회할꺼니까 일단 괄호 열어주자
for (Iterator q = ch.begin(); q != ch.end(); q++) {
if (q != ch.begin()) cout << " "; // q가 첫 자식이 아니면 앞에 출력된 애랑 띄어쓰기!!
parenPrint(T, *q); // 다음 자식 방문
}
cout << ")"; // 자식 순회 끝났으니까 괄호 닫기
}
}
후위 순회(Postorder Traversal)
후위 순회는 루트의 자식 노드를 루트로 하는 서브 트리를 먼저 재귀적으로 순회한 후에 루트를 방문한다.
그러니까 전위 순회가 루트 -> 왼쪽 자식들 -> 오른쪽 자식들 이었는데
후위 순회는 왼쪽 자식들 -> 오른쪽 자식들 -> 루트 이다!!!
Algorithm postorder(T, p):
for each child q of p do
recursively traverse the subtree rooted at q by calling postorder(T, q)
perform the "visit" action for node p후위 순회의 실행 시간 분석은 전위 순회의 실행시간 분석과 유사하다. 알고리즘의 비재귀적인 부분에서 소비된 총 시간은 트리 내의 각 노드의 자식 노드들을 방문하는 데 소비된 시간에 비례한다. 따라서 n개의 노드를 가진 트리 T의 후위 순회는 각 노드의 방문 시간이 O(1)이라고 가정할 떄 O(n)의 시간이 걸린다.
후위 순회를 하면서 노드가 방문될 때 각 노드에 저장된 원소를 출력하는 postorderPrint()함수를 만들어보자!!
void postorderPrint(const Tree& T, const Position& p) {
PositionList ch = p.children(); // 자식 리스트
for(Iterator q = ch.begin(); q != ch.end(); q++) {
postorderPrint(T, *q);
cout << " ";
}
cout << *p; // 자식들 다 방문하고 노드 방문해서 원소 출력
}후위 순회 함수는 트리의 각 노드 p에 대해 어떤 특성을 계산할 때, p의 특성을 계산하기 위해서는 p의 자식 노드에 대한 똑같은 특성이 이미 계산되어져 있는 것을 요구하는 문제를 풀기 위해 유용하다!! 무슨 말인지 아래 예를 보자!!

각 디렉토리에 이용되는 디스크 공간을 계산한다고 생각해보자. 디스크 공간은 아래의 합에 의해서 재귀적으로 구해진다.
- 디렉토리 그 자체의 크기
- 디렉토리 내에 있는 파일들의 크기
- 자식 디렉토리에 사용되는 공간
이 계산은 트리 T의 후위 순회로 구할 수 있다. 내부 노드 p의 서브 트리를 순회한 후에, p의 각 내부 자식 디렉토리에 의해 이용된 공간에 디렉토리 p 자체의 크기와 p안에 있는 파일들의 크기를 더하여 p에 이용된 공간을 계산할 수 있다.
말로 쓰니까 뭔가 어려운거 같은데 엄청 당연한 말을 어렵게 하고 있는거다!!! 어떤 디렉토리가 사용하는 공간을 알고싶으면 당연히 그 디렉토리안에 있는 각 파일들과 서브 디렉토리의 크기를 안 후에 얘네 둘을 더하고 이 디렉토리 자체의 크기까지 더하면 되는!!! 그런거!!! 이 알고리즘을 코드로 나타내보자!!!
int diskSpace(const Tree& T, const Position& p) {
int s = size(p); // p의 사이즈를 알아냄. 이 디렉토리가 가지고 있는 자체의 크기!! 파일과 서브 디렉토리 공간이 포함되지 않은
if (!p.isExternal()) { // 만약 p가 내부노드라면
PositionList ch = p.childe(); // p의 자식들을 리스트에 저장
for (Iterator q = ch.begin(); q != ch.end(); q++) // 자식들 순회
s += diskSpace(T, *q); // 서브트리들의 디스크 공간을 더함. 파일이라면 external이니까 파일 자체의 공간이 더해질 것이고 디렉토리라면 external이 아니니까 또 그안에 있는 그 밑의 서브 디렉토리, 또는 파일 공간이 더해질 것이고!!
cout << name(p) << ": " << s << endl; // 결과 출력
}
return s;
}참고 문헌
[1] Michael T. Goodrich, Roberto Tamassia, Davaid M. Mount, C++로 구현하는 자료구조와 알고리즘, WILEY, 2013.
'2022 > 자료구조 + 알고리즘' 카테고리의 다른 글
| [자료구조] 힙 (0) | 2022.01.18 |
|---|---|
| [자료구조] 우선순위 큐 (0) | 2022.01.16 |
| [자료구조] 이진 트리 (0) | 2022.01.14 |
| [자료구조] 분석 도구 (0) | 2022.01.06 |
| [자료구조] 링크드 리스트 (1) | 2022.01.06 |
블로그의 정보
공부 기록
너나나